Make mérés Convenient, Part 2.

Mondás:
Az a pince, amiben nincs bor, az nem pince, csak gödör.

Azok a - még a Rákócziak idején tufába vájt - pincék igazi borospincék, ott Tállyán például...

Lemerülünk:

Látogatók által itthagyott érmék, és a botritisz:

Nem whiskey, de nem ám! Édes furmint:

Egy apró szelete a tájnak, ahonnan származik:

És a mérésnek:

És a gondoknak:

Mert mit látunk a fenti fotón? A kontroller lekerült a GPS tartórúdjáról és valaki azzal legyez a magaslesen.
GPS mérésben jártas azonnal rávágná: nincs korrekció ott, ahol a GPS antenna áll és igaza van.
Ilyenkor egyet tehet az ember, keres egy helyet, ahol a kontroller veszi a mobil hálózaton (interneten), esetleg rádióhullámokon érkező korrekciós jelet, és imádkozik, hogy a GPS feldolgozó egysége ne legyen bluetooth távolságon túl. Szerencsére - bár küzdöttünk mint malac a jégen - még 150 méterre is volt kapcsolat és be tudtunk mérni minden pontot.
(Ugye milyen jól jön az, amikor a vevő nincs az antennába építve?)

Node miért is fontos az a korrekciós adat?
Ki küldi?
Miért?
És főleg: mi a szerepe a GPS rendszerben?

Az előző blogbejegyzésben megismertük azt, hogy miként határozzuk meg a pillanatnyi pozíciónkat a GPS (Global Positioning System) segítségével. Az ott leírtak alapján, a nem részletezett hibákkal terhelt koordinátáink nagyjából 3-10 méter pontossággal mutatják meg azt, hogy épp hol tartózkodunk.(Abba most nem megyünk bele, hogy mi az a koordináta, milyen koordináta-, vagy vetületi rendszerek és egyéb ilyen huncutságok léteznek.)
Ez a pontosság bőven elég ahhoz, hogy beforduljunk a keresett utcasarkon, megtaláljuk a korábban megjelölt horgászhelyünket, vagy eljussunk valakihez, aki megadta a saját pozíciójának koordinátáit.
De mit tehetünk, ha ennél pontosabb adatokra van szükségünk, ha mondjuk azt szeretnénk megtudni, hogy a szomszéd telkének határa tényleg ott van ahova leverte a kerítésének karóit, vagy mondjuk 20-30 centivel a mi telkünkre nyomult?
Ebben az esetben szükségünk lesz valamire, ami a leolvasott koordinátáinkat méter, vagy akár centiméter alatti pontosságra növeli.
Ehhez gyakorlatilag egy ismert koordinátájú pontra, egy ott elhelyezett GPS vevőre és valamiféle kommunikációra lesz szükségünk.

Ha tudjuk azt, hogy adott távolságon belül ugyanazokkal a hibákkal terhelt az összes GPS vevő számított koordinátája, akkor könnyű megérteni azt is, hogy egy ismert (és pontos, korábban valakik által meghatározott) koordinátán álló GPS vevő pontosan tudja azt, hogy adott pillanatban a GPS rendszer szolgáltatta koordináta és az álláspont pontos koordinátája között mekkora az eltérés vízszintes és magassági értelemben.
Jó kis tőmondat lett.
Ha tehát egy GPS vevő ismeri azt az eltérést, ami az adott rendszerben a pontos koordináta és a GPS rendszer koordinátája között fennáll, és azt az eltérést eljuttatja az összes körülötte elhelyezkedő GPS vevőhöz, azok mikroszámítógépe képes azt feldolgozni és a saját pozícióját megjavítani, vagyis pontosítani.
Ezzel az összes olyan GPS, amely vette az ismert pozícióban álló GPS vevő sugározta korrekciós jelet, szintén pontos koordinátákkal rendelkezik majd.
(Persze csak egy adott távolságon belül.)

Most már csak az a kérdés, hogy miként juttatjuk el a korrekciót a többi GPS vevőhöz.
Ehhez a referencia ponton álló GPS vevőt ki kell egészíteni egy rádióadóval, adó antennával, az összes többi GPS-nek pedig rendelkeznie kell egy rádióvevővel és ugye antennával, nem beszélve a kiegészítőkről.
Egy tipikus mobil referencia GPS így néz ki, miután találtunk egy ismert koordinátájú pontot - ez épp valahol Kurdisztánban - (és befutott a pizzafutár is):

Egy hasonló felállás (pizza nélkül), Algériában:

Itt pedig egy tipikus mozgó (rover) GPS-t láthatunk (Garry a texasi geodéta mozgatja), amely veszi a korrekciós jelet a referencia GPS-től, ezzel akár centiméteres pontossággal határozza meg helyzetét:

Persze ha OmniStar korrekciót használunk, nincs szükség rádió antennára, mert a referencia ebben az esetben egy geostacionárius pályán keringő műholdról érkezik, és a GPS antenna (egybeépítve a rádió vevővel, modemmel) azt a korrekciót használja (Marokkó):

Eddig megvolnánk...
Tehát a korrekciós adatok érkezhetnek műholdról, fix állomásokról, rádiójellel vagy mobilhálózat segítségével interneten keresztül. Mindegyik megoldásnak van előnye, és hátránya is, pl. nincs térerő, fedett a terület (fák, épületek blokkolják a jelet, kint vagyunk a sivatag közepén, stb.), így mindig az adott terület alapján határozzuk meg az alkalmazandó korrekciós adót.
Ezek lehetnek:
- Műholdról érkező korrekciós jel (OmniStar, EGNOS, WAAS, stb.)
- Földi fix pontokról rádión sugárzott korrekciós jel (DGPS)
- Földi fix pontokról mobilhálózaton/interneten sugárzott korrekciós jel (NTRIP)
- Földi ismert pontról sugárzott korrekciós jel (RTK rádióadóval felszerelt referencia pont segítségével)


Huh! Egyelőre ennyit a nőkről.
Nem tettem említést a nagy pontosságú utófeldolgozásos mérésekről, a GNSS (amerikai) és a GLONASS (orosz) műholdak mellett megjelent és használható egyéb GPS megoldásokról (pl. Galileo, Copernicus, GOVSATCOM, stb.), és még kismillió ezzel kapcsolatos dologról, de asszem így is elég unalmasra sikeredett ez a rész.
Is.
Ezért hát zene!

Make mérés Convenient, Part 1.

Haljon meg a lovam, ha nem így mondja!
Tessék:

Nyilvánvaló, hogy kényelmessé szeretnék tenni a mérést (egyáltalán, mindenféle munkát), azért vannak a mérnökök (leglustább népség az ismert univerzumban).
No és a fordítók.
Bocsánatos bűn az, hogy nem jön mindig minden össze elsőre, mint esetünkben a GPS kontroller indító képernyőjén.
A lényeg úgy is mögötte rejlik, magában a rendszerben. Mert ha tényleg kényelmessé teszi a measurementet, amely jelen esetben koordináta meghatározás GPS segítségével, akkor egy szavunk sem lehet.

Na de mi is az a GPS?
Hát ez, vágja rá az egyszeri autós:

Vagy ez, mondja a telefonhuszár:

vagy ez, feleli egy hajó navigátora:

vagy ez, morogja egy katona:

és mindenkinek igaza van (persze nincs igaza, mert NEM ez a GPS, de ez most mellékes).
Mint láttuk, számtalan formában előfordulhat, alkalmazzák hajókon, repülőgépeken, gépkocsikban, bombákban, telefonokban, mezőgazdasági gépeken, karórákban és még számos területen. A mikroelektronika folyamatos fejlődésével a készülékek egyre kisebbé és olcsóbbá válnak és ma már elérhetőek bárki számára, egyes típusok kezelése pedig nem bonyolultabb, mint mondjuk egy mobiltelefon használata.

A geodéziai GPS-ek (na ez sem pontos kifejezés, de konyhanyelven elmegy) nagyjából így néznek ki:

Egy rúdra rögzített GPS vevőből (GPS antenna, jelfeldolgozó egység, akksik és még pár úri huncutság egybe gyúrva) és egy -szintén a rúdra cuppantható -, azt vezérlő mézga féle kézi készülékből (kontroller) áll a legegyszerűbb és mégis hatékony rendszer (egymással akár vezetéken, akár bluetoothon kommunikálhatnak). Ugyan a Holdat látjuk felette a fotón, de ez ne tévesszen meg senkit, nem azzal kommunikál a szerkentyű. Egyszerűen épp ott mászkált, amikor felnéztem az égre.

Persze nekünk nem az igazi, hanem műhold, sőt műholdak kellenek ahhoz, hogy mérni tudjunk, azokból sem akármilyen, hanem speciálisan navigációs célra kifejlesztett, vagyis GPS műholdak.
Mostanában az amerikai cuccok már a harmadik generációnál tartanak (evolúció) és nagyjából így néznek ki:

Most egy kissé beleássuk magunkat a rendszer működésébe, vagyis megtanulhatjuk azt, hogy miként működik ez a fehér mágia. Ez aztán abban is segít(het), hogy tudjuk, mit kell tennünk ha épp akadozik a vétel, vagy miért nem 20 centire, 2 centire, vagy 2 milliméterre pontosak a koordinátánik.
Akit nem érdekel, az lapozzon a zenére (akit az sem: Alt+F4).

ELŐSZÓ
(vagy mi)

Ez számomra elég könnyű lesz, mivel régesrégesrég írni kezdtem egy könyvet ezekről a cuccokról (akkor még nem volt hazai forgalomban ilyesmi), csak épp elszólított a kötelesség (magyarul: lusta voltam befejezni), így copy/paste következik.
Bár az írás még a második generációs műholdak idejére datálódik úgy 2002 környékén - sok minden változott azóta -, az elv ma is ugyanaz.
Csapjunk bele!

Megjegyzés:
Baromi hosszú lesz és unalmas.


Még egy megjegyzés:
Én szóltam.


Bevezető szövegelés

Az emberek nagy része már az ősidőktől kezdve fontosnak tartotta tudni azt, hogy merre járt korábban, hol tartózkodik pillanatnyilag és merre kell haladnia ahhoz, hogy elérje úti célját.
Gondoljunk csak a tengereket járó hajósokra, a távoli idegen területekre eljutó katonákra, vagy kereskedőkre. Kezdetben talán kövekkel, ágakkal jelölték meg őseink a kalandozás közben megtett utat, emigyen bebiztosítva magukat, hogy visszataláljanak a táborukhoz.
Az ismert helyeket kitaposott ösvényeken, majd később kövekkel kirakott utakon érhették el és amíg nem tértek le azokról, nem volt gond az utazással.
Persze ez a fajta megoldás nem működött a sivatagokban, vagy a tengereken, hiszen a homok pillanatok alatt betemethette az út egy-egy szakaszát, a nyílt tengeren pedig végképp lehetetlen volt időtálló jeleket hagyni.
Az iránytű, a szeksztáns és a nagyon pontos óra (kronométer) megjelenése, valamint az egyre több ismert területet lefedő térképek sokat segítettek, de nem mindig tudtak feleletet adni arra a kérdésre, hogy hol is vagyunk éppen és hogyan is juthatunk el úti célunkhoz, elég ha csak arra gondolunk hogy a szeksztánst nem használhatták akkor, ha az eget felhők borították.

A kezdetek

A rádió feltalálásával a helymeghatározás fejlődésnek indult, megjelentek azok a készülékek, amelyek képesek voltak meghatározni egy adott rádióadó irányát.
Kettő, vagy több ilyen készülék mérési irányainak metszéspontjában pedig kisebb-nagyobb hibával meg lehetett határozni a térképen, illetve a valóságban a keresett adó helyét.
Felmerült a kérdés: ha megfordítjuk ezt az elvet, két vagy több ismert helyzetű adó által sugárzott jelből meg lehetne-e határozni a saját pozíciónkat?
A válaszra a tudósok igennel feleltek, és bár pl. az Angliát éjszaka bombázó német repülőgépek alkalmazták is ezt az eljárást, a pillanatny helyzetünk pontos meghatározása nagy távolságok esetén így sem oldódott meg. 1940-re tehető az a dátum, amikor egy globális helymeghatározó és navigációs rendszer létrehozásának ötlete felmerült, persze a technikai korlátok a megvalósítást akkor még nem tették lehetővé.

Az 50-es és 60-as években még égetőbbé vált az a probléma, hogy mindig tudjuk azt, hol tartózkodunk éppen és erről másokat is informáljunk (vagy épp ellenkezőleg, titkoljuk azt).
Gondoljunk csak a hihetetlenül megnövekedett légi, vagy tengeri forgalomra, de legfőképpen mint minden új találmány iránt fogékony szervezetre: a hadseregre.
A rakétákat hordozó atommeghajtású tengeralattjáróknak több hetes víz alatti cirkálás után is pontosan kellett ismerniük tartózkodási helyüket ahhoz, hogy parancs esetén végrehajthassák feladatukat, vagyis kilőjjék rakétáikat.
Az űrtechnika fejlődése új lehetőségeket tárt fel a helymeghatározás területén a '70-es években. Az Egyesült Államok - valamint az akkori Szovjetúnió - rendelkeztek azokkal a szükséges erőforrásokkal, amelyek egy új, minden eddiginél hatékonyabb rendszer kifejlesztéséhez elengedhetetlenek. A katonák olyan navigációs rendszert akartak, amely a nap 24 órájában használható, az időjárástól függetlenül pontosan és megbízhatóan meg tudja mondani azt, hogy hol tartózkodnak pillanatnyilag.
Az SR-71-es kémrepülőgép csillagok alapján dolgozó navigációs rendszere tudta ezt, de az ugye a felhők felett repült...

1973-ban kezdődött az a program, amelyben az Egyesült Államok légiereje, szárazföldi hadserege és haditengerészete, valamint a Védelmi Térképészeti Iroda összefogott, hogy létrehozzon egy nagy pontosságú, űrbázisú navigációs rendszert.
Felállították a GPS Joint Office nevű katonai szervezetet, amelyhez később 9 NATO ország csatlakozott.
Kezdetben tisztán katonai vállalkozásnak indult a dolog, de szinte naponta növekedett a civil felhasználók és alkalmazások köre.
A GPS nem csak hihetetlenül pontos idő, sebesség és koordináta adatokat szolgáltatott, hanem - mivel rádióhullámokkal működik -, hozzáférhetővé vált széles rétegek számára is.

Ez lett az a rendszer, amelyet az angol GPS rövidítés alapján manapság mindenki csak úgy ismer, hogy „dzsi-pi-esz”, és amely a ”Global Positioning System” (Globális Helymeghatározó Rendszer) rövidítése. Ez az összetett rendszer lehetővé tette a katonai, valamint a civil területeken történő, elsősorban navigációs jellegű alkalmazást, és a kalandozók egyik régi álma valóra válhatott: GPS-szel a kezünkben mindig tudjuk azt, hogy merre jártunk, hol vagyunk és merre induljunk tovább, hogy úti célunkat elérjük.
A GPS egyik nagy erőpróbájához az 1991-es Öböl Háború adott hátteret, ahol az egységek már fel voltak szerelve kézi vevőkészülékekkel. A rendszer hatékonyságához elég ha idézünk egy a harcokban résztvevő brit tisztet: "Az angol hadsereg egész története során most tudta először pontosan azt, hogy hol is tartózkodik pillanatnyilag."

Természetesen mint nagyhatalom, a volt Szovjetúnió sem mondhatott le a GPS fejlesztéséről és kialakította saját rendszerét, amely a '80-as évek végétől elérhetővé vált a civil szféra számára is. Ettől az időtől számítva tehát gyakorlatilag két különböző GPS rendszer működött.
Az amerikai Nemzetvédelmi Minisztérium felügyelete alá tartozó globális helymeghatározó rendszer neve NAVSTAR GPS, ennek orosz felügyelet alatti megfelelője a GLONASS GPS.
Készültek olyan GPS vevőkészülékek, amelyek képesek a két különböző renszer jeleinek vételére, feldolgozására. Tervek születtek közös európai, csak polgári célú rendszerek kifejlesztésére is (NAVSAT, PRARE), de könyvünkben írásunkban - mivel ezen rendszert használó készülékek a legelterjedtebbek - csak az amerikai NAVSTAR GPS rendszert tárgyaljuk, így GPS alatt a továbbiakban ezt kell értenünk.
(Azóta, mint tudjuk, már élnek a kínai műholdak is és egy csomó szolgáltató tette lehetővé a műholdas referencia szolgáltatást (pl. OmniStar), így akár egy, arra alkalmas készülékkel is pontos koordinátát kaphatunk szinte bárhol a világban.)

Magyarországon 1990-ben jelentek meg az első kézi GPS vevők, valamint a főleg geodéziai célokra kifejlesztett rendszerek.
Azon szerencsések közé tartoztam, akiknek módjukban állt ilyen technikával dolgozni 1992-től, és mai napig emlékszem arra a Magellán kézi vevőkészülékre, amellyel akkor ott, Tunézia sivatagos területein navigáltunk.



A GPS működésének alapjai

Ha kezünkbe veszünk egy GPS készüléket és bekapcsoljuk, a szoftver inicializálása után a legutolsó bekapcsoláskor letöltött almanach file alapján azonnal keresni kezdi a pillanatnyilag elérhető, tehát a horizont fölött tartózkodó műholdakat.
Ebből adódik egy esetleges probléma: ha hosszú ideig nem kapcsoltuk be a vevőnket, vagy kb. 200km-nél távolabbra utaztunk annak kikapcsolása után, akkor több időt vesz igénybe az aktuális pozíciónk meghatározása.
Erről - vagyis az inicializálás befejezéséről - valamilyen formában információt kapunk a vevőkészülék kijelzőjén, amely alapvetően megegyezik, bármely gyártó bármely típusával is rendelkezünk.
Nézzük csak miről is informál bennünket az alábbi képen látható GPS készülék (az első Garminom valamikor 1997-ből)

A bal felső sarokban a 3D NAV arról tájékoztat, hogy legalább 4 megfelelően elhelyezkedő műholddal van adatkapcsolatunk, vagyis háromdimenziós koordinátát kapunk, tehát földrajzi szélességet és hosszúságot, valamint magasságot.
A jobb felső sarokban az EPE az angol Estimated Position Error (várható pozició hiba) röviditése, vagyis a helyzetünk ekkora hibával lesz terhelt, ami jelen esetben 6m pontatlanságot jelent a vízszintes koordinátákban és ennek kb. 1.5 szeresét a magasságban.
A bal oldali sötét oszlop az elemek töltöttségéről tájékoztat az F és az E vagyis a Full (tele) és az Empty (üres) között, gyakorlatilag úgy, ahogy egy gépkocsi üzemanyagszintjelzője mutatja a még rendelkezésünkre álló nafta mennyiségét. (Ez azért fontos, mert villany nélkül halott a GPS, megszűnik a navigáció ezen formája és ha épp a Szaharában bóklászunk távol a tábortól, jobb, ha szedjük a lábunkat abban az esetben, ha elfelejtettünk bepakolni elég elemet, akksit, mifenét.)
A tőle jobbra látható nyillal átszúrt N (North) (figyelem, ez NEM iránytű!) azt jelöli, hogy ha a készüléket ez alapján úgy fordítjuk, hogy a nyíl a valós észak felé mutat, akkor a két koncentrikus kört tartalmazó „égi térkép”-ről leolvashatjuk a pillananyilag a horizont fölött tartózkodó GPS műholdak közelítő helyzetét.
A külső kör a horizontot jelképezi, a belső kör a horizont fölötti 45 fokot, a középpont pedig az ég fejünk feletti pontját. Az elszórtan látható számok egy-egy GPS műholdat jeleznek, és a holdakat ezen számok alapján azonosítjuk.
A fotón például a 21-es műhold majdnem pontosan fölöttünk van pillanatnyilag, a 6-os keletre és körülbelül 45 fok magasságban a horizont fölött, a 3-as pedig vagy éppen most emelkedett a horizont fölé, vagy éppen most fog a horizont alá bukni nyugaton, attól függően hogy milyen irányban mozog.
Az inverzben látható műholdakkal valamilyen oknál fogva nincsen adatkapcsolat (a képen a 2-es, 10-es és a 17-es).
Ez alapján a "térkép" alapján tudjuk azt, hogy melyik műhold lehet épp takarásban, így annak esetlegesen hozzánk csak visszaverődve eljutó jelei pozíció hibát okozhatnak.
Lehet hogy csak egy épület takarja őket, de az is lehet, hogy pillanatnyilag kikapcsolták őket. Természetesen a műholdak nagy sebességgel mozognak, igy 15-20 perc múlva már teljesen átrendeződik a képernyő: lesz műhold, amely eltűnik a horizont alatt és lesz új, amely a látóhatár fölé emelkedik, így biztosítva az állandó, a navigációhoz szükséges legalább 4 hold jelenlétét, szakszerű nevén a lefedettséget.

Alul szintén láthatjuk az összes műholdat és itt függőleges oszlopok jelzik az adatkapcsolatot, az adott műholdhoz kapcsolódó oszlop magassága pedig a vett jel erősségéről tájékoztat (a képen a 21-es hold jele a legerősebb, a 15-ös és a 25-ös pedig a leggyengébb).
A készülék bekapcsolásakor ez a mező üres, csak az elméletileg a horizont fölött látható műholdak sorszámai látszanak. Ahogy a GPS készülék felismeri a műholdakról beérkező jeleket, úgy jelenik meg egy-egy oszlop az adott műholdat jelképező szám fölött. Ezzel kezdetét veszi a vevő és a műhold közötti kapcsolatfelvétel, vagy más néven szinkronizálás, amelynek befejeztével az adott műhold addig világos oszlopa sötétre vált és megfelelő számú műhold adatainak vétele esetén megkapjuk pillanatnyi koordinátánkat.
Ahhoz hogy a vízszintes koordinátáinkat ki tudja számolni a mikroprocesszor, legalább három műhold adatait kell hogy vegye a készülék. Ha a tengerszint feletti magasságunkat is tudni szeretnénk, ahhoz egy negyedik műhold is szükséges.
Ez a minimális követelmény, természetesen az a jó, ha ennél több műholdról kapunk adatokat, hiszen egyrészt a műholdak hozzánk viszonyított elhelyezkedése - szakszóval a műhold geometria - nagyban befolyásolja pillanatnyi helyzetünk pontosságát, másrészt ha mozgunk, esetleg takarásba kerülhet egy-egy műhold és ez a pozíciónk elvesztésével járhat.
Persze manapság ez már nem jelenthet problémát, hiszen a fenti képen is tíz műhold látszik a horizont fölött, de pl. 1992-ben örültünk annak, ha pár órára legalább 4 műhold jeleit tudtunk venni.

Megkaptuk tehát a pillanatnyi helyzetünk koordinátáit, de mit is kezdhetünk vele? Először is eltárolhatjuk egy gombnyomással, hiszen minden kézi GPS készülék, még az órákba épített legkisebb is képes memóriájától függően rögzíteni bizonyos számú pozíciót (általában útpontnak, waypointnak nevezve). Eltárolhatunk bármit, legyen az egy horgászhely, egy erdei pihenő, egy parkoló, vagy bármi egyéb, számunkra fontos hely.
Ha van eltárolt koordinátánk, akkor a GPS készülékkel bármikor megtalálhatjuk azt a helyet, legyen koromsötét éjszaka, köd, teljesen ismeretlen vidék, vagy akár valamelyik tenger közepe.


Ha valahova el szeretnénk jutni, de még sohasem jártunk ott, ebben is segít a GPS. Nincs más dolgunk, mint a készülék billentyűzete segítségével bevinni úticélunk koordinátáit, és arra irányt és távolságot kérve már indulhatunk is, csak a képernyőn megjelenő navigaciós utasításokat kell követnünk.

A harmadik fontos dolog amit megtehetünk, hogy utunk során folyamatosan rögzítjük pozíciónkat (track külföldiül), így ha esetleg eltévednénk, bármikor vissza tudjuk követni azt. Ezzel a módszerrel és megfelelő szoftverrel akár térképre is rajzolhatjuk később a pontokat, így kiegészítve azt új információkkal, vagy egy laptopon, palmtopon megjelenített térképen akár valós időben nyomon követhetjük azt, hogy épp merre mozgunk.
Biztosak lehetünk abban, hogy a GPS készülékünkkel mindig tudni fogjuk azt, hogy hol vagyunk, azt hogy milyen irányba kell mennünk ha el szeretnénk jutni egy másik, ismert koordinátájú helyre, és hogy merre jártunk addig, amíg eljutottunk egyik helyről a másikra. (Azt hogy ”mindig”, fenntartással kezeljük, de erről majd később ejtünk szót.)

Az újabb vevőkön ezen kívül találhatunk még elektronikus iránytűt és barometrikus magasságmérőt is, amelyek sok esetben nagyban megkönnyíthetik a navigációt. Ezen információkon túl még kapunk néhány számunkra talán fontos adatot a GPS készüléktől, mint pl. mennyi a pontos idő, hiszen atomórákkal áll kapcsolatban; mikor kel, vagy nyugszik a Nap illetve a Hold az adott helyen, mennyi a pillanatnyi sebességünk, vagy mekkora a távolság két eltárolt pont között.
Hogy hogyan is kapjuk meg mindezeket, ennek járunk utána a következő fejezetekben.


Mi is az a GPS rendszer?

A rendszert három fő részre oszthatjuk, mégpedig az űr-, az ellenőrző és a felhasználói szegmensre.

Az űrszegmens

Ezt a szegmenst alkotják a GPS műholdak, amelyekből 24 aktív és néhány tartalék kering a Föld körül. A műholdak legfontosabb részei az atomórák, pontosabban fogalmazva az oszcillátorok, amelyekből minden egyes Block II-es hold négy darabot szállít a pontosság és megbízhatóság érdekében (kettő cézium, kettő pedig rubídium oszcillátor).
Fontos alkotóelem még a különböző kódokat generáló számítógép, valamint a rádiófrekvenciás adó- és vevőmodulok.
A műholdakon melegítő egységek és hővisszaverő szigetelés biztosítják az oszcillátorok optimális működéséhez elengedhetetlen stabil hőmérsékletet. Az "(űr)járművek" 3 dimenziós stabilizáló rendszerekkel vannak ellátva, amelyek segítségével a napelemek mindig merőlegesen állnak a napsugarakra, és az adó és vevőantennák a Föld felé mutatnak.
Mindezek mellett az összes GPS műholdat ellátták az esetleges nukleáris robbanást érzékelő egységgel is, "sosem lehessen tudni" alapon. (Az idézet a Misimesemackóból származik, 2007-es bejegyzés)
A fotón egy Block IIR-es műhold látható:

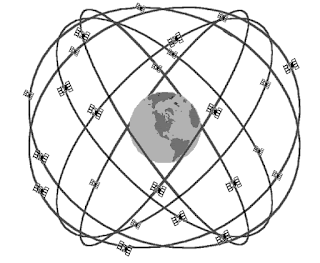
A műholdak (az angol elnevezésük ”Space Vehicle” után SV-ként rövidítve) nagyon magas (20183 Km) orbitális pályán keringenek, amely pályák 55 fokos hajlásszöget zárnak be az egyenlítő síkjával.
Hat darab pálya, egymástól 60 fokra elforgatva fedi le a Földet, mindegyiken 4 darab műhold kering 90 fokos szögtávolságra egymástól, valamint néhány tartalék az esetlegesen meghibásodó, vagy ideiglenesen kikapcsolt holdak kiváltására.
Egy-egy műholdnak 4 perccel kevesebb mint 12 órára van szüksége ahhoz, hogy megtegyen egy teljes fordulatot, ezzel biztosítva a folyamatos lefedettséget, valamint azt a sebességet, amely a megfelelő pontosságú mérésekhez elengedhetetlen. Utóbbi azért fontos, hogy egy adott földi pont beméréséhez sok eltérő mérési eredmény átlagát számolhassuk, ezzel növelve a pontosságot. Ilyenkor általában 15 vagy 30 másodpercenként rögzítünk egy-egy "adatcsomagot" a műholdakról, ez alatt azz idő alatt már elég nagy utat tesznek meg ahhoz, hogy ne azonos adatokkal számoljunk pl. ITRF mérés során
Érdekesség, de ha 50km-rel magasabb pályára állítanák a műholdakat, az a 4 perces időkülönbség - amely a 24 órás solar óra és a 24 órás sideral óra közötti eltérésből adódik - eltűnne, ezzel azonban a rendszer folyamatos elfordulása, mozgása megszűnne.

A régebbi műholdakat fokozatosan lecserélik az újabb Block II R holdakra, amelyek a Block II-es holdak modernizált változatai. Ezek már a sokkal stabilabb hidrogén mézert használják a cézium/rubidium oszcillátorok helyett, emellett fejlett önálló navigációs tulajdonságokkal rendelkeznek. Emellett egy újabb civil, és két új katonai kódót adtak hozzá az eddig használatos kódokhoz, valamint megnövelték a lehetséges kimenő jelerősséget és ezek a műholdak már képesek újra konfigurálni mind a kódot, mind pedig annak erősségét, ha szükséges.
Mivel egymás között is kommunikálnak, ezért nem csak ön-navigációra képesek, hanem másféle űrjárműveknek is képesek adatokat szolgáltatni a helymeghatározáshoz, vagyis a GPS navigáció „kiléphet” az űrbe.
A rendszerhez tartozó 12 műhold teljes modernizálásának és szolgálatba állításának ideje várhatóan 2006 lesz.
A fejlődés azonban nem áll meg, a Lockheed Martin és az ITT Industries már most dolgoznak a következő generációs műholdakon, amelyekre mint GPS III-ra hivatkoznak.

Az ellenőrző szegmens

Az ellenőrző szegmens részei a Föld különböző pontjain elhelyezkedő megfigyelő-, illetve vezérlőállomások, amelyekből jelenleg 5 darab működik:

Az adatok feltöltését végző fő ellenőrző/irányító állomás (Master Control Station, vagy MCS) Colorado Springs-ben, a Schriever légi bázison található.
Mellette négy megfigyelő állomás (Diego Garcia, Ascension szigetek, Kwajalein és Hawaii) követi és veszi folyamatosan a műholdakról érkező jeleket, gyűjt meteorológiai adatokat és továbbítja azokat a fő irányító állomásra. Az MCS végzi a folyamatosan változó ionoszférikus modellek kiszámítását, a műholdak óra korrekcióinak elvégzését és a műholdakra vonatkozó parancsok meghatározását.
Az itt kiszámított pálya és óra adatokat, korrekciókat azután a fő állomás és adóantennával is rendelkező követő állomások (Diego Garcia, Ascension szigetek, Kwajalein) szabályos időközönként feltötik a megfelelő műholdaknak.

A felhasználói szegmens

Ezen szegmens részei a GPS vevőkészülékek, azok szoftverei, valamint az egyéb olyan állomások, amelyek korrekciós jeleket sugározva lehetővé teszik az arra alkalmas vevőkészülékek számára a méteres, vagy még pontosabb helymeghatározást (pl. Magyarországon az NTRIP).


A pozíció meghatározása, avagy hogyan működik a GPS?

A pozíció meghatározásához használt technika meglepően egyszerű: meg kell mérnünk a távolságunkat a GPS műholdaktól, majd a geodéziában alkalmazott “hátrametszés ismert távolság alapján” képletének felhasználásával kiszámíthatjuk a térbeli koordinátáinkat.
Ehhez azonban még néhány feltételnek teljesülnie kell, nevezetesen: a földi GPS vevő belső órája pontosan egy időben kell hogy ”üssön” az űrben száguldó GPS műholdakon található atomórákkal és legalább három műholdat kell hogy észleljünk adott időpillanatban.
Ezután már pofonegyszerű meghatározni a helyzetünket, de nézzük csak, hogyan is történik ez a gyakorlatban.

Ha tudjuk azt, hogy egy adott GPS műhold (nevezzük 1-esnek), milyen messze található tőlünk, akkor máris elmondhatjuk azt, hogy az univerzum egy viszonylag kis területén tartózkodunk. Egy olyan gömb felületén állunk valahol, amelynek középpontjában az ismert koordinátájú műhold áll, a gömb sugara pedig a műhold és a köztünk lévő távolság.

Azt persze nem tudhatjuk hogy a gömb melyik részén tartózkodunk, hiszen csak a műhold távolságát ismerjük, az irányát pedig nem, ezért ugyanebben az időpillanatban mérjük meg egy másik GPS műhold távolságát is (2 számú műhold). Ekkor már leszűkítettük a tartózkodási helyünket a gömbfelületről egy kör kerületére, amely kör a két különböző műholdközéppontú gömb metszési síkjában keletkezik.

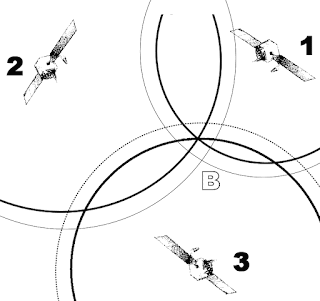
Ha pontosan ekkor egy harmadik GPS műholdtól (3-as számú) is megmérjük a távolságunkat, akkor annak a gömbje két ponton fogja metszeni az előbb kapott metszési kört annak kerületén (A és B pontok), ezzel biztosan kijelenthetjük azt, hogy mi ezen két pont egyikén tartózkodunk.

Egy negyedik GPS műhold pontosan megmutatná azt, hogy a két pont közül melyik az ”igazi”, de erre a gyakorlatban nincs szükség, hiszen az egyik pont vagy túlságosan messze esik a Földtől, vagy pedig ésszerűtlenül nagy sebességgel mozog (ne felejtsük el, a GPS rendszer műholdjai nem geostacionárius pályán állnak, hanem folyamatosan és nagy sebességgel keringenek a Föld körül, tehát a példánkban szereplő A és B pont közül az egyik mindenképpen mozogni fog).
A GPS vevőkészülékekbe épített számítógép többféle módon is képes meghatározni azt, hogy melyik a helyes pozíció a lehetséges két pont közül, így elmondhatjuk azt, hogy a pillanatnyi helyzetünk meghatározásához elvileg elégséges három műhold pontos távolságának ismerete.
Ez az állítás persze csak elméletileg igaz, később látni fogjuk majd, hogy miért van feltétlenül szükség egy negyedik műholdra is ahhoz, hogy pontos, három dimenziós (x,y,z) koordinátát kapjunk.
Eljutottunk tehát addig a pontig, ahol már tudjuk azt, hogy a helyzetünk meghatározásához az első és legfontosabb lépés a GPS vevőnk és a GPS műholdak közötti távolság meghatározása, lássuk tehát, hogy miként "mérjük" meg azt.

A távolságmérés

A GPS műholdaktól való távolság meghatározása a fény terjedési sebességének felhasználásával történik.
A fény adott közegben állandó sebességgel terjed, (mondhatjuk úgy is, hogy a fény egy stabil frekvencia), tehát a sebesség, valamint az út megtételéhez szükséges idő alapján számolható a megtett távolság.
Egy elektrooptikai távmérővel könnyen meg tudjuk határozni a távolságot, mivel a méréshez használt sugár (infravörös, lézer, stb.) a műszerből indul és egy speciális prizmáról (vagy akár egy tereptárgyról) visszaverődve oda is érkezik vissza. Az ábrán A-val jelöltük a távmérőt és B-vel a prizmát, amelyről a mérőjel visszaverődik a műszerbe.

Ebben az esetben tehát a méréshez használt jelet sugárzó adó és a visszavert jelet érzékelő vevő azonos helyen tartózkodik, leggyakrabban egy készülékbe építve. Így nincs más dolgunk, mint egy megfelelően pontos órával megmérni a jel kibocsátása és annak visszaérkezése között eltelt időt, majd azt megszorozni a fénysebességgel és megkapjuk a jel által megtett utat, vagyis a távolságot. Persze a kapott eredményt még el kell osztanunk kettővel, hiszen ez alatt az idő alatt a mérőjel kétszer tette meg az utat a műszer és a prizma között.
Ezek alapján a képlet:

a/ Mért idő=T2-T1

ahol:
T1=jel kibocsátásának ideje a távmérő adó részén
T2=jel visszaérkezésének ideje a távmérő vevő részén

b/ Távolság=(Mért idő x Fénysebesség)/2

A GPS-szel történő távolság meghatározás esetén rádióhullámokat használunk jelként, amelyek szintén fénysebességgel terjednek, így a képletet itt is alkalmazhatjuk, némi változtatással.

GPS esetén azonban az adó (az ábrán A-val jelzett műhold) és a vevő (B-vel jelzett vevőkészülék) különböző helyen tartózkodik, a műholdról induló jel nem tér vissza a műholdhoz, pályafutása befejeződik amint eléri a GPS vevőt, tehát az elektrooptikai távmérőhöz képest a képlet így módosul:

a/ Mért idő=T2-T1

ahol:
T1=a jel kibocsátásának ideje a GPS műholdon
T2=a jel beérkezésének ideje a GPS vevőkészüléken


b/ Távolság=Mért idő x Fénysebesség


Ahhoz hogy egy ilyen passzív rendszerben meg tudjuk mérni a jel kibocsátása és annak a vevőhöz történő beérkezése között eltelt időt, két órára lesz szükségünk, az egyik az adón (vagyis a GPS műholdon), a másik pedig a vevőn (a GPS vevőkészüléken) kell hogy helyet kapjon.
Emellett szükségünk lesz egy kódolt jelre, amely az adott műholdat is azonosítja.
A műhold órája ismeri a jel generálásának és elküldésének pillanatát, a vevő órája pedig tudja azt, hogy mikor érkezett meg az az adott jel, amelyet egyébként ő is pontosan ugyanabban a pillanatban generál.
A két különálló óra kommunikál egymással: a GPS jelnek hordoznia kell azt az információt, amely elmondja a vevőnek azt a pontos időpillanatot, amikor a jel elhagyta a GPS műholdat.
Ha egy adott jelsorozatot egyazon időpillanatban generál a GPS műhold és a vevőkészülék is, akkor ha összehasonlítás céljából egymásra fektetjük azokat, a GPS-ről érkező jelsorozat „késésben” lesz a vevő által generált jelsorozathoz képest. Ez az időbeni elcsúszás pontosan olyan mértékű, mint amennyi ideig a jel utazott a műholdtól a vevőig.
A jel sebessége ismert (fénysebesség), most már tudjuk az utazáshoz szükséges időt is, és így már könnyen kiszámíthatjuk a távolságot a műhold és a vevő között.
Ugye milyen egyszerű?

Hát nem...
Az elmondottakból tisztán látszik az, hogy nem elég a két óra önmagában, nagyon fontos, hogy teljesen szinkronizáltak legyenek, vagyis pontosan egyszerre ”üssenek”, mert csak ez garantálja a két jel azonos időpillanatban történő létrehozását, és ugye ez a GPS-szel történő távolságmérés alapja.
Ennek nézünk most utána.


Az órahiba meghatározása

Mint tudjuk, a GPS műholdak atomórákat (sic!) hordoznak a fedélzetükön, a mi GPS vevőnk viszont csak egy átlagosan pontos kvarcórát kapott, valami olyasmit, amelyet számtalan formában a kezünkön is hordunk (mint már említettük, bár óráknak nevezzük őket, jelen esetben mégis pontosabb lenne a megfogalmazás, ha oszcillátornak hívnánk ezeket a készülékeket).
Az anyagilag és fizikailag is kivitelezhetetlen, hogy a vevőkészülékekbe is atomórák kerüljenek, hiszen egy hátizsák pénz nem lenne elég ahhoz, hogy megvegyünk egy hidrogén mézer oszcillátort, ám ha mégis megvennénk, a hátizsákunk nem lenne elég ahhoz, hogy cipeljük azt.
És akkor még nem beszéltünk a működtetéshez szükséges feltételek megteremtéséről.

Mivel a tökéletes szinkronizálás ilyen módon nem biztosítható, ezért matematikailag kell megoldani a problémát, hiszen pl. 1 mikromásodperc eltérés a két óra között 300m hibát jelentene a távolságmérésben. (Legyen 1 ezredmásodperc eltérés a két óra között és ez a hiba rögtön 300km-re emelkedik.)
Most jön el az ideje annak a korábban már említett negyedik GPS műholdnak, amely az órák szinkronizálását fogja végezni.
Mint azt már tudjuk, három műhold elméletileg elégséges a pozíciónk meghatározásához, de ez csak akkor igaz, ha mind az adó, mind a vevő órája szinkronban dolgozik, vagyis teljesen egy időpillanatban mondják azt, hogy tikk (és takk).
A trigonometria törvénye alapján ha 3 pontos mérés meghatározza egy pont helyzetét a térben, akkor 4 hibával terhelt mérés esetén kiszűrhető a hiba, ha a hiba azonos mértékű volt minden egyes mérésnél.
Esetünkben ez a hiba a GPS vevőkészülék órájának (oszcillátorának) pontatlansága miatt keletkezik, tehát egyformán terheli a GPS műholdakról beérkező összes jelet.
A helymeghatározásba bevonva egy negyedik műholdat, az óraeltérés miatt keletkező hiba kiejthető és megvalósul az adó(k) és a vevő órájának szinkronizálása.

Bár a GPS három dimenziós rendszer, egyszerűbb két dimenzióban szemléltetni a szinkronizálást az érthetőség kedvéért. Mivel a mért távolságot gyakorlatilag a jel kibocsátása és beérkezése között eltelt idő határozza meg, használjuk inkább az időt a távolság helyett a példában a könnyebb érthetőség kedvéért.
Az első ábra szemlélteti azt a helyzetet, amikor mind a GPS műholdak, mind a GPS vevő órája szinkronizálva van, 5 másodperc távolságra vagyunk az 1-es számú műholdtól és 7 másodpercre a 2-es számútól. Ebben az esetben a számított pozíciónk tökéletesen egybeesik azzal a ponttal ahol állunk, és az ábrán A-val jelöltük.

Tegyük fel, hogy a GPS vevőnk belső órája kissé siet a GPS műholdak óráihoz képest, és mivel hosszabb ideig ki volt kapcsolva, így az utolsó szinkronizálás óta (tehát amikor még együtt "ütött" a GPS műhold atomórájával) összegyűjtött 1 másodperc eltérést.
Ez azt jelenti, hogy bekapcsolás után, amikor mi azt olvasnánk le a kijelzőn, hogy a pontos (GPS) időnk 12:00:00, akkor a műholdak atomórái még csak 11:59:59-nél járnak.
Ebben az esetben az előző ábrához képest a számított pozíciónk teljesen máshova kerülne, mivel a jel kibocsátása és beérkezése között most 6 másodperc lesz az 1-es műhold esetén és 8 másodperc a 2-es számú műhold esetén.
A jel utazási ideje megnőtt, tehát a műhold és a vevő közötti távolság is megnőtt és így most a B-vel jelzett pontba számolná a készülék a helyzetünket (halványabb kör):

Ha történetesen egy térkép van a kezünkben és tudjuk azt, hogy a keresett koordinátának egy útkereszteződésben kell lennie, ellenben a GPS vevőnk egy tó közepére irányít bennünket, akkor rögtön felismernénk azt, hogy valami nem tökéletes, bár tenni nem tudnánk semmit ellene.
Ha ez a félrepozícionálás tengeren, sivatagban, levegőben, vagy a világűrben történne, annak akár végzetes következményei is lehetnének.

Most hívjuk segítségül a trigonometriát, és a kétdimenziós vázlatunkba vegyünk be egy harmadik műholdat is, amely három dimenziós helymeghatározás esetén a negyedik GPS műholdat jelentené. Legyen ez a műhold a 3-as számú, és erről 6 másodpercig utazzon a rádióhullám a GPS vevőnkig. Ha tökéletes lenne a műholdak és a vevő készülékünk szinkronizálása, akkor az első ábrán látható rajz így egészülne ki a harmadik műholddal, és megerősítené a jó pozíciónkat az A pontban:

Mivel azonban a GPS vevőnk órája még mindig 1 másodpercet siet, így a 3-as műholdról érkező jel is módosul 6-ról 7 másodpercre.
Mint látható, az 1-es és 2-es műholdról érkező adatok alapján a B pont még mindig jónak tűnik, azonban az fizikailag lehetetlen, hogy a 3-as műhold jelei alapján számolt kör kerülete metsze az előző két műhold által meghatározott pontot (pontozott kör):

Minden GPS vevő úgy van programozva, hogy azonnal riadót fújjon, amint egy mérési sorozat eredményei (az összes rádiókapcsolatban álló műholdról érkező távolság adat) nem metszik egymást. Rögtön arra "gondol", hogy az ő belső órája nincsen szinkronban a GPS műholdak óráival.
Igy aztán rögtön elkezd hozzáadni (vagy levonni) azonos időmennyiségeket az általa követett műholdak jeleihez egészen addig, amíg az összes mérés eredménye egy pontban metszi egymást.
Példánkban ez azt jelenti, hogy elvesz mindhárom műholdról beérkező jelből 1 másodpercet, vagyis meghatározza hogy az ő órahibája +1 másodperc.
A GPS vevőnk számítógépe gyakorlatilag nem céltalanul keresgél, algebrai úton, négyismeretlenes egyenlet segítségével nagyon gyorsan megtalálja az órahibát.
A vevőkészülék természetesen azonnal elvégzi saját belső óráján a korrekciót, amint meghatározta az eltérést a GPS idő és a saját belső órája között, így a képernyőre pillantva már a pontos (nagyon pontos) időt fogjuk látni, amely a GPS műholdak atomóráihoz igazodik.
Ezzel elértük azt, hogy a kis vacak, vevőbe épített kvarcóra pontosan együtt ketyeg az űrben keringő és baromidrága atomórákkal.
Áldásbékesség!
De most ugrik a majom a vízbe!


A távolság meghatározásához szükséges adatok

A GPS műholdak a távolság meghatározásához kétféle kódot sugároznak amelyek P, avagy precíz kódok, illetve C/A, vagy durva (coarse) kódok.
Mindkét kód annyira bonyolult, hogy gyakorlatilag először csak elektromágneses zajoknak tűnnek az éterben, közös nevük is erre utal: PRN kódok az angol “PseudoRandom Noise” rövidítése alapján amit talán „álvéletlen zajként” lehetne ferdíteni.
Valami ilyesmit képzeljünk el:

Szép, ugye?
Persze az elnevezésük ne tévesszen meg bennünket, hiszen ezek nem véletlenszerűen keltett zajok, hanem épp ellenkezőleg: nagyon gondosan meghatározott kódok, mivel ismételhetőnek és helyettesíthetőnek kell lenniük.
A GPS műholdak a következő ábrán látható jeleket sugározzák:

A P (precíz vagy pontos) kód másodpercenként 10,23 millió bit sebességgel érkezik és mind az L1 (1575,42MHz), mind az L2 (1227,60MHz) frekvenciákon sugározzák a műholdak, segítségével 30cm-es pontosság érhető el. A P kód 2 a 48.-on -1 (értsd: kettő a negyvennyolcadikon mínusz 1) bit hosszú, ami időben kifejezve 266 nap, amely 37 részegységre osztott és ezek a részkódok egy-egy műholdhoz vannak rendelve.
Minden GPS műhold 7 napig ismétli a saját P kódját (a GPS időskála szerint vasárnap 0 órától kezdődően), és az egész kód megújul minden 37. héten. Mivel a P kódot minden műhold ugyanazon a frekvencián sugározza, valahogy meg kell különböztetni egymástól a GPS holdakat.
Egyik módja ennek az, hogy hozzákapcsolnak egy-egy hetet a 37 ciklusból egy-egy műholdhoz. Igy például a 14-es műhold (SV14) azért 14-es, mert a 14. heti P kódot sugározza, az SV2-es műhold a 2. heti P kódot és így tovább.
A P kódot titkosítani is lehet egy A kódnak nevezett bináris kóddal, ennek katonai felhasználás esetén van jelentősége. Itt jegyezzük meg, hogy az egyszerű GPS vevők nem képesek feldolgozni a P kódot, így azokkal nem érhető el az előbb említett precizitás.

A C/A (durva vagy pontatlan) kód csak az L1-es frekvencián érkezik, tízszer lassabb mint a P kód, így 3m-es pontosságra elegendő.
Ez a kód csak 2013 bit hosszú és folyamatosan, 1 milliszekundumonként ismétlődik. Ezzel a kóddal egyszerű a műholdak azonosítása, mivel minden műholdnak saját és a többiétől teljesen különböző C/A kódja van.

A GPS holdakról érkezik egy harmadik kódsorozat is, amelyet Navigációs kódnak, vagy D kódnak neveznek és bár közvetlenül nem vesz részt a távolság meghatározásában, mégis nagyon fontos adatokat hordoz. A Navigációs kód alacsony frekvenciás (50MHz) jel és az L1 és L2 frekvenciákon van modulálva. Hossza 1500 bit, öt információs blokkra osztották:
- óra korrekció
- ephemeris adat (műhold koordináták)
- ephemeris adat (műhold koordináták)
- ionoszférikus adatok, antispoofing (P kód változtatása Y kódra, ami még biztonságosabb), almanach adatok a tartalék műholdakról (SV25-SV32)
- almanach adatok, műholdak pillanatnyi állapota (működik, nem működik, stb.)



A távolság meghatározása

Tudjuk tehát, hogy a GPS műholdak folyamatosan sugározzák a PRN kódokat és a Navigációs kódot. A GPS vevőkészüléknek nem kell mást tennie, mint folyamatosan venni legalább négy műhold rádió jeleit, generálni ugyanazt a PRN kódot a saját processzorával, majd addig csúsztatni előre-hátra azt egy kódkövető hurok segítségével, amíg a műholdról érkezett kód és a GPS vevőkészülék által generált kód nem fedi egymást.
Az első ábrán nincsen fedés a műholdról érkezett illetve a vevő által generált jelek között:

Itt már közelít egymáshoz a két jelsorozat:

Teljes az átfedés, a vevő beazonosította a műholdról érkező jelet:

Mivel a GPS műhold(ak) és a GPS vevő órái (oszcillátorai) egyazon időpillanatban kell hogy generálják ugyanazokat a kódsorozatokat, a műholdról érkező jelek “késésben” lesznek a vevő által generált jelekhez képest. Ez a késés formájában megjelenő időkülönbség megegyezik azzal az idővel, amely alatt a jel megtette az utat a műholdtól a vevőig.
Az adott műhold távolságát tehát megkapjuk, ha ezt a "késési" időegységet megszorozzuk a rádióhullám terjedési sebességével, vagyis a fénysebességgel. A kapott eredményt persze még módosítanunk kell néhány, a terjedési sebességet befolyásoló értékkel annak érdekében, hogy pontosabb eredményt kapjunk, de gyakorlatilag megérkeztünk: kiszámítható a pillanatnyi koordinátánk.

Egyszerűsítve tehát a vevő az alábbiak szerint határozza meg a koordinátáit:

1 - PRN és D kódok vétele legalább 4 GPS műholdról, a vevő és a GPS műhold óráinak szinkronizálása

2 - A műholdaknak megfelelő PRN kódok generálása a vevőn

3 - A generált és a beérkezett kódsorozatok összehasonlítása, a generálás és beérkezés közötti időintervallum meghatározása, ezzel pedig minden egyes (látható) műhold távolságának kiszámítása (időkülönbség szorozva a fény terjedési sebességével)

4 - Az ionoszférikus és toposzférikus javításokkal, órakorrekciókkal, stb. módosítani a kiszámított távolságokat

5 - A műholdak ismert koordinátái és a hozzájuk tartozó távolság alapján a megfelelő egyenletekkel kiszámitani a GPS vevő x,y,z koordinátáit a WGS-84 koordináta rendszerben, vagyis Szélesség, Hosszúság, Ellipszoid magasság.

És ezzel már meg is kapjuk/rögzíthetjük a kábeldob melletti elektróda koordinátáit, amint odarakjuk a GPS antenna rúdját, vízszintbe állítjuk a libellát és megnyomjuk a mérés gombot a kontrolleren (ha épp az a feladat):

Nade!
(Most ugrik a majom a vízbe)
Hogyan lesz a nagyjából 5 méteres pontosságból - mert ugye alapból kb. ekkora hibával kapjuk meg a vevő pozícióját - pár centiméteres precíz, ismételhető (ez nagyon fontos) eredmény?
A következő blogbejegyzés majd megmondja! (sátáni - egyre halkuló - kacaj)




Addig is: zene!

Izgalmas...

Hát hogy a fenébe ne lenne izgalmas, amikor azt hallja az ember fia, hogy Elektromos Ellenállás Tomográfia (ERT). Hát még ha tapogatja is, no nem a tomográfiát, de az ahhoz sszükséges cuccokat.
És hogy mire való?
Sokmindenre, vágja rá a nagytudású egy szóba tömörítve, kibontva pedig, többek között a gátak alatt esetleg megbúvó vízelvezető rétegek felderítésére.
Aszondod az nem fontos?
Hát hogy a rákba ne lenne fontos, ha teszem azt megindul az áradás, a gát ugyan állja a sara... izé vizet, visszatartja egészen addig, amíg a tetejéig ér (tuti van erre faszányosan megfogalmazott vízügyes szó is). Na de mi történhet, ha mondjuk a régi meder valahol ott kacskaringózott és ott lapul alant a vízáteresztő réteg?
Mindenki elképzelheti...
Nekünk pl. egyszer régesrég egy messzi, tunéziai galaxisban az egyik korrekciós szondánk számára lefúrt lyukban megjelent a víz.
A megjelent azt takarja, hogy feljött megnézni, ki az ördög munkálkodik ott?
Aztán mivel a rétegnyomás olyan volt, mégtöbb víz jött fel nézelődni.
Hiába tömedékeltük el a lyukat, a víz akkor már baromira kíváncsi volt arra, hogy mi folyik ott fent (nem is csoda, ha mondjuk évszázezredekig be volt zárva a sötétbe).
Hiába cementeztünk, építettünk rá betonalapot, hívtunk piócás embert, a víz csak jött és jött...
Ha betömtük középen, feltűnt a jobb oldalon, ha ott is betömtük, megjelent a bal oldalon, ha azt is betömtük, még balabbra kezdett szivárogni, kikerülve a cementezett részt.
Végül feladtuk, nem volt mit tenni, hagytuk, hogy egy szép nagy tó kerekedjen a sivatagban...

Na most ugyanezt képzeljük el itt: a gát fogja az áradást, az meg szépen alatta megkeresi az utat és hogy napirajzosra vegyem a témát:

Na hát ezért vagyunk most itt, a Tisza gátján, ezért rakjuk le az érzékelőket és ezért tikk-takkoljuk meg az alattunk húzódó rétegeket ebben a szép, melegnek nem mondható, ellenben fagyos időben.

Persze először ki kell nyitni a kapukat ahhoz, hogy nekuessünk a serénykedésnek, mert ilyenkor még friss a tomográfia, nem beszélve a dolgozó népről:

Mire észbe kapunk, már a fél vonal kiterítődött, mert a tomográfia azt szereti:

Csipeszek az elektródán, hogy majd a törzskábelről érkező delej tomográfoljon. Vagy valami ilyesmi.
Az okosok szerint:
A multielektródás geoelektromos szelvényezés az egyenáramú elektromos geofizikai mérések közül a legkorszerűbb. Ennek során a felmérendő szelvény mentén fém elektródákat verünk a talajba, amelyeket "inteillgens" elektromos kábel köt össze a mérőműszerrel. A terítés teljes hossza a kutatási mélységtől függ és akár több száz méter is lehet.

Persze geodézia nélkül mit sem ér az egész, itt épp nigériai és mongol geofizikus palánták készülnek bemérni az elektródák helyét:

Hogy az android mire (is) képes:

Közben persze a műszer dolgozik, küldi a jelet, veszi a jelet, tomografál:

Aztán a nap végén összeszedjük az összes kábelt, elektródát, csipeszt (persze nem ennyi az annyi, ez csak egy a sok csomag közül):

Minden a kocsikon, bevonulunk a panzióba egy istenes pinceperkelt (marhából, gombával, ahogy illik) összerittyentésére, mert most annak jött el az ideje, a tomográf most aluszik, máma már nem reped tovább...
Vagy az egy másik vers?

Zene: